資訊內容
100行Python代碼,輕松搞定神經網絡

大數據文摘出品
來源:eisenjulian
編譯:周家樂、錢天培
用tensorflow,pytorch這類深度學習庫來寫一個神經網絡早就不稀奇了。
可是,你知道怎么用python和numpy來優雅地搭一個神經網絡嘛?
現如今,有多種深度學習框架可供選擇,他們帶有自動微分、基于圖的優化計算和硬件加速等各種重要特性。對人們而言,似乎享受這些重要特性帶來的便利已經是理所當然的事兒了。但其實,瞧一瞧隱藏在這些特性下的東西,能更好的幫助你理解這些網絡究竟是如何工作的。
所以今天,文摘菌就來手把手教大家搭一個神經網絡。原料就是簡單的python和numpy代碼!
文章中的所有代碼可以都在這兒獲取。
https://colab.research.google.com/github/eisenjulian/slides/blob/master/NN_from_scratch/notebook.ipynb
符號說明
在計算反向傳播時, 我們可以選擇使用函數符號、變量符號去記錄求導過程。它們分別對應了計算圖中的邊和節點來表示它們。
給定R^n→R和x∈R^n, 那么梯度是由偏導?f/?j(x)組成的n維行向量
如果f:R^n→R^m?和x∈R^n,那么?Jacobian矩陣是下列函數組成的一個m×n的矩陣。
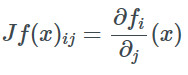
對于給定的函數f和向量a和b如果a=f(b)那么我們用?a/?b?表示Jacobian矩陣,當a是實數時則表示梯度
鏈式法則
給定三個分屬于不同向量空間的向量a∈A及c∈C和兩個可微函數f:A→B及g:B→C使得f(a)=b和g(b)=c,我們能得到復合函數的Jacobian矩陣是函數f和g的jacobian矩陣的乘積:
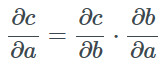
這就是大名鼎鼎的鏈式法則。提出于上世紀60、70年代的反向傳播算法就是應用了鏈式法則來計算一個實函數相對于其不同參數的梯度的。
要知道我們的最終目標是通過沿著梯度的相反方向來逐步找到函數的最小值 (當然最好是全局最小值), 因為至少在局部來說, 這樣做將使得函數值逐步下降。當我們有兩個參數需要優化時, 整個過程如圖所示:

反向模式求導
假設函數fi(ai)=ai+1由多于兩個函數復合而成,我們可以反復應用公式求導并得到:
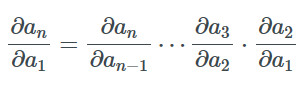
可以有很多種方式計算這個乘積,最常見的是從左向右或從右向左。
如果an是一個標量,那么在計算整個梯度的時候我們可以通過先計算?an/?an-1并逐步右乘所有的Jacobian矩陣?ai/?ai-1來得到。這個操作有時被稱作VJP或向量-Jacobian乘積(Vector-Jacobian Product)。
又因為整個過程中我們是從計算?an/?an-1開始逐步計算?an/?an-2,?an/?an-3等梯度到最后,并保存中間值,所以這個過程被稱為反向模式求導。最終,我們可以計算出an相對于所有其他變量的梯度。
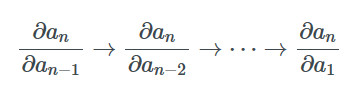
相對而言,前向模式的過程正相反。它從計算Jacobian矩陣如?a2/?a1開始,并左乘?a3/?a2來計算?a3/?a1。如果我們繼續乘上?ai/?ai-1并保存中間值,最終我們可以得到所有變量相對于?a2/?a1的梯度。當?a2/?a1是標量時,所有乘積都是列向量,這被稱為Jacobian向量乘積(或者JVP,Jacobian-Vector Product?)。
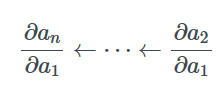
你大概已經猜到了,對于反向傳播來說,我們更偏向應用反向模式——因為我們想要逐步得到損失函數對于每層參數的梯度。正向模式雖然也可以計算需要的梯度, 但因為重復計算太多而效率很低。
計算梯度的過程看起來像是有很多高維矩陣相乘, 但實際上,Jacobian矩陣常常是稀疏、塊或者對角矩陣,又因為我們只關心將其右乘行向量的結果,所以就不需要耗費太多計算和存儲資源。
在本文中, 我們的方法主要用于按順序逐層搭建的神經網絡, 但同樣的方法也適用于計算梯度的其他算法或計算圖。
關于反向和正向模式的詳盡描述可以參考這里?
http://colah.github.io/posts/2015-08-Backprop/ ?
深度神經網絡
在典型的監督機器學習算法中, 我們通常用到一個很復雜函數,它的輸入是存有標簽樣本數值特征的張量。此外,還有很多用于描述模型的權重張量。
損失函數是關于樣本和權重的標量函數, 它是衡量模型輸出與預期標簽的差距的指標。我們的目標是找到最合適的權重讓損失最小。在深度學習中, 損失函數被表示為一串易于求導的簡單函數的復合。所有這些簡單函數(除了最后一個函數),都是我們指的層, 而每一層通常有兩組參數: 輸入 (可以是上一層的輸出) 和權重。
而最后一個函數代表了損失度量, 它也有兩組參數: 模型輸出y和真實標簽y^。例如, 如果損失度量l為平方誤差, 則?l/?y為 2 avg(y-y^)。損失度量的梯度將是應用反向模式求導的起始行向量。
Autograd
自動求導背后的思想已是相當成熟了。它可以在運行時或編譯過程中完成,但如何實現會對性能產生巨大影響。我建議你能認真閱讀 HIPS autograd的 Python 實現,來真正了解autograd。
核心想法其實始終未變。從我們在學校學習如何求導時, 就應該知道這一點了。如果我們能夠追蹤最終求出標量輸出的計算, 并且我們知道如何對簡單操作求導 (例如加法、乘法、冪、指數、對數等等), 我們就可以算出輸出的梯度。
假設我們有一個線性的中間層f,由矩陣乘法表示(暫時不考慮偏置):
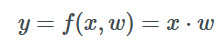
為了用梯度下降法調整w值,我們需要計算梯度?l/?w。這里我們可以觀察到,改變y從而影響l是一個關鍵。
每一層都必須滿足下面這個條件: 如果給出了損失函數相對于這一層輸出的梯度, 就可以得到損失函數相對于這一層輸入(即上一層的輸出)的梯度。
現在應用兩次鏈式法則得到損失函數相對于w的梯度:
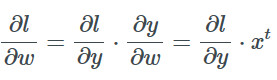
相對于x的是:
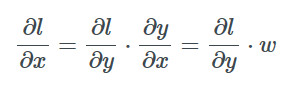
因此, 我們既可以后向傳遞一個梯度, 使上一層得到更新并更新層間權重, 以優化損失, 這就行啦!
動手實踐
先來看看代碼, 或者直接試試Colab Notebook
https://colab.research.google.com/github/eisenjulian/slides/blob/master/NN_from_scratch/notebook.ipynb
我們從封裝了一個張量及其梯度的類(class)開始。
現在我們可以創建一個layer類,關鍵的想法是,在前向傳播時,我們返回這一層的輸出和可以接受輸出梯度和輸入梯度的函數,并在過程中更新權重梯度。
然后, 訓練過程將有三個步驟, 計算前向傳遞, 然后后向傳遞, 最后更新權重。這里關鍵的一點是把更新權重放在最后, 因為權重可以在多個層中重用,我們更希望在需要的時候再更新它。
class Layer:def __init__(self):self.parameters = []def forward(self, X):"""Override me! A simple no-op layer, it passes forward the inputs"""return X, lambda D: D
def build_param(self, tensor):"""Creates a parameter from a tensor, and saves a reference for the update step"""param = Parameter(tensor)self.parameters.append(param)return param
def update(self, optimizer):for param in self.parameters: optimizer.update(param)
標準的做法是將更新參數的工作交給優化器, 優化器在每一批(batch)后都會接收參數的實例。最簡單和最廣為人知的優化方法是mini-batch隨機梯度下降。
class SGDOptimizer():def __init__(self, lr=0.1):self.lr = lrdef update(self, param):param.tensor -= self.lr * param.gradientparam.gradient.fill(0)
在此框架下, 并使用前面計算的結果后, 線性層如下所示:
class Linear(Layer):def __init__(self, inputs, outputs):super().__init__()tensor = np.random.randn(inputs, outputs) * np.sqrt(1 / inputs)self.weights = self.build_param(tensor)self.bias = self.build_param(np.zeros(outputs))def forward(self, X):def backward(D):self.weights.gradient += X.T @ Dself.bias.gradient += D.sum(axis=0)return D @ self.weights.tensor.Treturn X @ self.weights.tensor + self.bias.tensor, backward
接下來看看另一個常用的層,激活層。它們屬于點式(pointwise)非線性函數。點式函數的 Jacobian矩陣是對角矩陣, 這意味著當乘以梯度時, 它是逐點相乘的。
class ReLu(Layer):def forward(self, X):mask = X > 0return X * mask, lambda D: D * mask計算Sigmoid函數的梯度略微有一點難度,而它也是逐點計算的:
class Sigmoid(Layer):def forward(self, X):S = 1 / (1 + np.exp(-X))def backward(D):return D * S * (1 - S)return S, backward當我們按序構建很多層后,可以遍歷它們并先后得到每一層的輸出,我們可以把backward函數存在一個列表內,并在計算反向傳播時使用,這樣就可以直接得到相對于輸入層的損失梯度。就是這么神奇:
class Sequential(Layer):def __init__(self, *layers):super().__init__()self.layers = layersfor layer in layers:self.parameters.extend(layer.parameters)def forward(self, X):backprops = []Y = Xfor layer in self.layers:Y, backprop = layer.forward(Y)backprops.append(backprop)def backward(D):for backprop in reversed(backprops):D = backprop(D)return Dreturn Y, backward
正如我們前面提到的,我們將需要定義批樣本的損失函數和梯度。一個典型的例子是MSE,它被常用在回歸問題里,我們可以這樣實現它:
def mse_loss(Yp, Yt):diff = Yp - Ytreturn np.square(diff).mean(), 2 * diff / len(diff)就差一點了!現在,我們定義了兩種層,以及合并它們的方法,下面如何訓練呢?我們可以使用類似于scikit-learn或者Keras中的API。
class Learner():def __init__(self, model, loss, optimizer):self.model = modelself.loss = lossself.optimizer = optimizerdef fit_batch(self, X, Y):Y_, backward = self.model.forward(X)L, D = self.loss(Y_, Y)backward(D)self.model.update(self.optimizer)return L
def fit(self, X, Y, epochs, bs):losses = []for epoch in range(epochs):p = np.random.permutation(len(X))X, Y = X[p], Y[p]loss = 0.0for i in range(0, len(X), bs):loss += self.fit_batch(X[i:i + bs], Y[i:i + bs])losses.append(loss)return losses
這就行了!如果你跟隨著我的思路,你可能就會發現其實有幾行代碼是可以被省掉的。
這代碼能用不?
現在可以用一些數據測試下我們的代碼了。
X = np.random.randn(100, 10)w = np.random.randn(10, 1)b = np.random.randn(1)Y = X @ W + Bmodel = Linear(10, 1)learner = Learner(model, mse_loss, SGDOptimizer(lr=0.05))learner.fit(X, Y, epochs=10, bs=10)
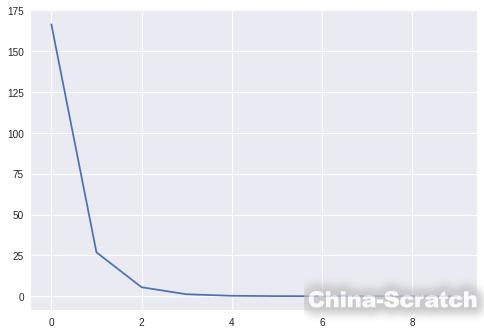
我一共訓練了10輪。
我們還能檢查學到的權重和真實的權重是否一致。
print(np.linalg.norm(m.weights.tensor - W), (m.bias.tensor - B)[0])> 1.848553648022619e-05 5.69305886743976e-06好了,就這么簡單。讓我們再試試非線性數據集,例如y=x1x2,并且再加上一個Sigmoid非線性層和另一個線性層讓我們的模型更復雜些。像下面這樣:
X = np.random.randn(1000, 2)Y = X[:, 0] * X[:, 1]losses1 = Learner(Sequential(Linear(2, 1)),mse_loss,SGDOptimizer(lr=0.01)).fit(X, Y, epochs=50, bs=50)
losses2 = Learner(Sequential(Linear(2, 10),Sigmoid(),Linear(10, 1)),mse_loss,SGDOptimizer(lr=0.3)).fit(X, Y, epochs=50, bs=50)
plt.plot(losses1)plt.plot(losses2)plt.legend(['1 Layer', '2 Layers'])plt.show()
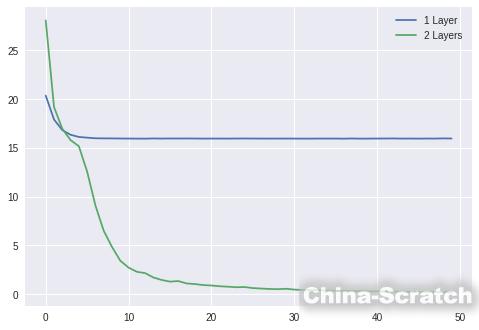
比較單一層vs兩層模型在使用sigmoid激活函數的情況下的訓練損失。
最后
希望通過搭建這個簡單的神經網絡,你已經掌握了用python和numpy實現神經網絡的基本思路。
在這篇文章中,我們只定義了三種類型的層和一個損失函數, 所以還有很多事情可做,但基本原理都相似。感興趣的同學可以試著實現更復雜的神經網絡哦!
References
[1] Thinc Deep Learning Library?
https://github.com/explosion/thinc
[2] PyTorch Tutorial?
https://pytorch.org/tutorials/beginner/nn_tutorial.html
[3] Calculus on Computational Graphs
http://colah.github.io/posts/2015-08-Backprop/
[4] HIPS Autograd?
https://github.com/HIPS/autograd
相關報道:
https://eisenjulian.github.io/deep-learning-in-100-lines/
實習/全職編輯記者招聘ing
加入我們,親身體驗一家專業科技媒體采寫的每個細節,在最有前景的行業,和一群遍布全球最優秀的人一起成長。坐標北京·清華東門,在大數據文摘主頁對話頁回復“招聘”了解詳情。簡歷請直接發送至zz@bigdatadigest.cn
志愿者介紹
后臺回復“志愿者”加入我們


聲明:本文章由網友投稿作為教育分享用途,如有侵權原作者可通過郵件及時和我們聯系刪除