scratch算法練習階乘求和

階乘是基斯頓·卡曼（Christian Kramp，1760～1826）于 1808 年發明的運算符號，是數學術語。

一個正整數的階乘（factorial）是所有小于及等于該數的正整數的積，并且0的階乘為1。自然數n的階乘寫作n!。1808年，基斯頓·卡曼引進這個表示法。亦即n!=1×2×3×...×n。

題目：求1+2!+3!+...+20!的和。

分析：新建三個變量：n作為自然數，取值從1到20 ；t為n的階乘，初識值為1，t=t*n；s為綜合，將t進行累加即可

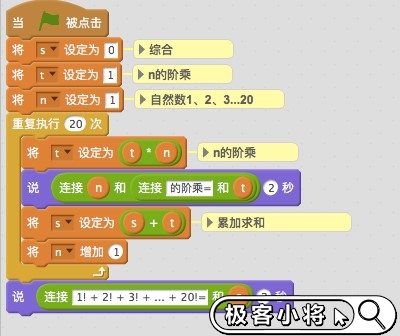
運行結果：1! + 2! + 3! + ... + 20! = 2561327494111820300 

注意：這個計算結果數據非常大，由于scratch自身原因，這個答案顯示是有誤差的，正確的答案應該是 2561327494111820313