前幾年，有本標(biāo)題略顯聳動(dòng)的書籍，題目叫《中國(guó)人的思維危機(jī)：中國(guó)教育扼殺了中國(guó)人的思維能力》（豆瓣評(píng)分6.2分）。

作者的文字流于表面上的情緒，但是里面對(duì)于中國(guó)人缺乏思維能力的結(jié)論，還是有很多人是贊同的。這本書的結(jié)論以《中國(guó)人思維的五大邏輯缺陷》在朋友圈流傳。

里面列舉了中國(guó)人比較常見的五大邏輯缺陷，包括：

• 概念模糊

• 不懂集合概念

• 類比推理，生拉硬扯

• 非黑即白，二元思維

• 亂立靶子，錯(cuò)誤推理

仔細(xì)想想，好像日常生活真的挺普遍的，再往前推論，其中一個(gè)重要原因在于，我們的孩子在受教育階段相對(duì)缺乏必要的思維訓(xùn)練。

聯(lián)合國(guó)教科文組織把邏輯列為7門基礎(chǔ)學(xué)科中的第二門，僅次于數(shù)學(xué)，《大英百科全書》也把它列為五門基礎(chǔ)學(xué)科之一，足見其重要性。可是，好似從來(lái)沒(méi)有見過(guò)哪個(gè)學(xué)校專門為其開設(shè)課程的。

今天就向大家推薦一部BBC出品、有關(guān)邏輯的紀(jì)錄片，名叫《邏輯的樂(lè)趣》。雖然只有短短一個(gè)小時(shí)，但相信看完之后，大家會(huì)對(duì)邏輯有個(gè)更深入的了解，同時(shí)也對(duì)如何培養(yǎng)孩子的邏輯思維能力，有一定的想法。

強(qiáng)烈推薦5歲以上的孩子看起來(lái)。

這部紀(jì)錄片通過(guò)詼諧幽默的方式，向大家介紹什么是邏輯以及邏輯的發(fā)展歷史，并在其間穿插了一些邏輯學(xué)的重要概念：三段論、布爾邏輯、弗雷格的形式系統(tǒng)、哥德堡不完備定理……等等等等，簡(jiǎn)直就是一部邏輯學(xué)概論加簡(jiǎn)史的概念。

到底啥是邏輯？

紀(jì)錄片一下來(lái)就為我們展現(xiàn)了邏輯在生活中的重要性。大到國(guó)家的政治生活，小到我們選擇走哪一條路最便捷，這些都離不開邏輯。

那到底啥是邏輯？抽象地說(shuō)，這些區(qū)分真話和假話的過(guò)程，我們認(rèn)為一種人類創(chuàng)造的最簡(jiǎn)單但最有力的工具，就是邏輯。

有點(diǎn)難懂？那用三個(gè)邏輯學(xué)家和一個(gè)酒館的例子來(lái)解釋一下。

話說(shuō)三位邏輯學(xué)家一同走進(jìn)一個(gè)酒吧。酒保問(wèn)：你們?nèi)欢夹枰【茊幔?

第一位邏輯學(xué)家略帶遲疑地說(shuō)：我不知道。

第二位邏輯學(xué)家看了看左右，也說(shuō)了聲：我不知道。

而第三位邏輯學(xué)家面帶微笑且肯定地說(shuō)：是的，我們都要啤酒。

當(dāng)看到這里的時(shí)候，網(wǎng)上驚起一片彈幕，都說(shuō)什么鬼？

主講人戴夫·克里夫透徹分析了這個(gè)邏輯學(xué)笑話后，我們恍然大悟。

酒保的問(wèn)題是：你們仨都需要啤酒嗎？

關(guān)鍵是“你們仨”。如果他們?nèi)齻€(gè)中的任何一個(gè)不想要啤酒的話，他就會(huì)回答“不”，這是因?yàn)椋绻渲幸粋€(gè)人不要啤酒，他們就不是“都要啤酒”。

第一位邏輯學(xué)家想要喝啤酒，但是他不能替其他人回答，所以他不得不說(shuō)“我不知道”。

相同的問(wèn)題落到了第二位邏輯學(xué)家身上，同理，他也會(huì)回答“不知道。”

第三位邏輯學(xué)家也想喝啤酒，他正確地從前兩位的回答中進(jìn)行推理，所以說(shuō)“是的，我們都要啤酒。”

那再次回到“邏輯”這個(gè)概念上，邏輯究竟是什么？

這次，戴夫·克里夫給了我們一個(gè)比較精確的定義：

邏輯不是知識(shí)，邏輯也不生產(chǎn)知識(shí)，它所做的就是給我們提供一套嚴(yán)謹(jǐn)?shù)囊?guī)則，用來(lái)組織和運(yùn)用知識(shí)。

聽起來(lái)，邏輯依然高深莫測(cè)。那就讓我們追溯歷史，從古希臘時(shí)期開始更深入地了解它。

有點(diǎn)復(fù)雜，不過(guò)這就是邏輯學(xué)的歷史

講到邏輯，就離不開亞里士多德著名的三段論。

問(wèn)題來(lái)了：什么是三段論？

三段論包含三個(gè)命題，前兩個(gè)命題是前提，這兩個(gè)前提是爭(zhēng)論雙方都承認(rèn)的事實(shí)。后一個(gè)命題是結(jié)論。

一個(gè)最經(jīng)典的三段論如下：

前提1：凡人必有一死

前提2：蘇格拉底是人。

結(jié)論：蘇格拉底必死。

三段論太經(jīng)典了，以至于兩千多年過(guò)去了都沒(méi)有人努力改變它。

直到19世紀(jì)40年代，一位英國(guó)數(shù)學(xué)家布爾的出現(xiàn)。

布爾邏輯

片中沒(méi)有講到的一個(gè)概念和區(qū)分，就是布爾之前的邏輯被稱為分析邏輯（還處于分析學(xué)的層面，從確鑿為真的前提出發(fā)，以獲取絕對(duì)真實(shí)），布爾之后的邏輯被稱為數(shù)理邏輯（邏輯可以用數(shù)學(xué)來(lái)表示）。

布爾在結(jié)合亞里士多德的三段論和代數(shù)方程組的過(guò)程中迸發(fā)了靈感。

他認(rèn)為邏輯學(xué)更接近數(shù)學(xué)而非哲學(xué)，于是人們可以將邏輯語(yǔ)言轉(zhuǎn)化為數(shù)字符號(hào)，然后就能像解方程式一樣解題。

為了更好來(lái)說(shuō)明布爾邏輯，片中用兩個(gè)非常形象的例子來(lái)說(shuō)明：

例子1:

比如X代表毛茸茸的東西，Y代表會(huì)叫的，布爾還弄出了一整套運(yùn)算符號(hào)來(lái)整合XY的關(guān)系，其中三個(gè)最重要的符號(hào)就是and, or not.

比如，X和Y的交集部分（X and Y），就是汪星人。

布爾邏輯的運(yùn)用，還有一個(gè)很天才、重要的應(yīng)用，就是如今的計(jì)算機(jī)運(yùn)行邏輯的基礎(chǔ)：

布爾邏輯中，任何關(guān)于對(duì)和錯(cuò)的說(shuō)明，可以用1和0指代。

主持人戴夫·克里夫還是用狗來(lái)舉例子。

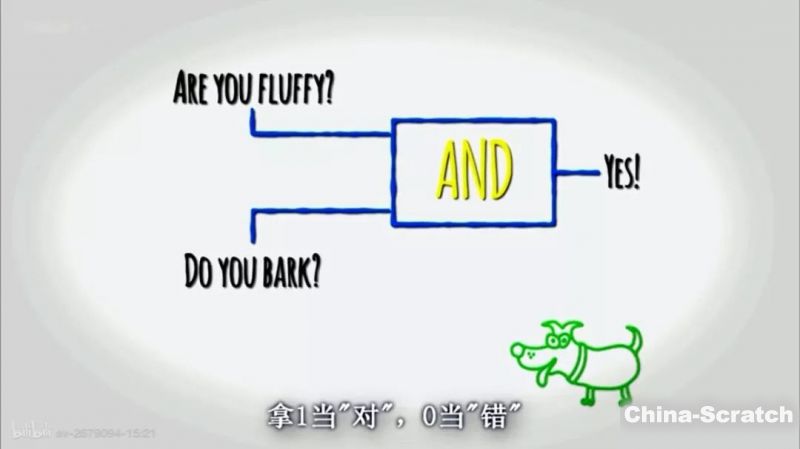
你有毛嗎？如果回答是yes，就用數(shù)字“1”來(lái)指代；你會(huì)汪汪嗎？如果回答是yes，也用數(shù)字“1”來(lái)指代。回答是no，就用“0”來(lái)指代。

在25個(gè)7歲孩子的幫助之下，克里夫教授還成功模擬了布爾邏輯的運(yùn)行方式。

但布爾邏輯不是完美無(wú)缺的，為了說(shuō)明這一點(diǎn)，片中的調(diào)皮的戴夫·克里夫教授，拿著一個(gè)牌子向路人詢問(wèn)：牌子上的話是對(duì)還是錯(cuò)。牌子上寫著“this sentence is false。”

額，這話該怎么回答：如果這句話是錯(cuò)的，那么它就是對(duì)的；如果他是對(duì)的，那他也一定是錯(cuò)的。這就是悖論。

到了19世紀(jì)晚期，像上面這句話類似的悖論，變成了一個(gè)非常棘手的難題，甚至威脅到了數(shù)學(xué)的根基，即第三次數(shù)學(xué)危機(jī)。

因此，人類必須尋找更新、更復(fù)雜的邏輯。后來(lái)的弗雷格，對(duì)這個(gè)問(wèn)題進(jìn)行了深入的鉆研。

弗雷格形式系統(tǒng)

與布爾不同，弗雷格認(rèn)為數(shù)學(xué)的基礎(chǔ)是邏輯，他立志要用精確的語(yǔ)法規(guī)則或者句法規(guī)則把他的概念文字發(fā)展成一種人工語(yǔ)言，進(jìn)而把邏輯推理發(fā)展成機(jī)械的演算，這就是所謂“弗雷格形式系統(tǒng)。”

但弗雷格還是沒(méi)有解決悖論問(wèn)題，羅素以更大的熱情接手了弗雷格的研究，甚至花了九年時(shí)間來(lái)證明1+1=2。

哥德爾不完全性定理

本來(lái)以為邏輯的大廈就要建成，但是一個(gè)幽靈，一個(gè)不確定性的幽靈在數(shù)學(xué)上空徘徊。

什么是不確定性呢？放心，作為一個(gè)走詼諧幽默風(fēng)、老少皆宜的紀(jì)錄片，當(dāng)然得用一個(gè)你我都懂得的彼方，來(lái)讓觀眾了解：

什么是不確定性？

眾所周知，反間諜組織的任務(wù)就是確保周圍沒(méi)有間諜滲入，但是如果反間諜組織的頭目是間諜呢？

邏輯學(xué)意義上的“不確定性”可以這樣理解：你在數(shù)學(xué)領(lǐng)域建立高墻，以防范不確定性之類的東西，但是正可能是這些高墻就讓矛盾出現(xiàn)了。

哥德爾提出：任何想成為數(shù)學(xué)基礎(chǔ)的邏輯系統(tǒng)，必須完整而且不矛盾，通過(guò)閱讀羅素的著作，發(fā)現(xiàn)了其中的矛盾。

他得出結(jié)論：在任何邏輯系統(tǒng)中，它不是不矛盾的，就是完整的，但是它不能同時(shí)擁有這兩種屬性。這就意味著在數(shù)學(xué)邏輯中存在一些真相的確是對(duì)的，但是永遠(yuǎn)不能被證明他是對(duì)的。這就是著名的哥德爾不完全性定理。

于是，對(duì)絕對(duì)真理的探索腳步暫時(shí)停止了。

圖靈開創(chuàng)的應(yīng)用邏輯學(xué)時(shí)代

但無(wú)心插柳柳成蔭，邏輯學(xué)的發(fā)展在理論層面和數(shù)學(xué)層面進(jìn)入瓶頸期，卻給英國(guó)邏輯學(xué)家、數(shù)學(xué)家圖靈以啟發(fā)。從他開始，邏輯學(xué)進(jìn)入了一個(gè)更加重視實(shí)踐的新紀(jì)元。

圖靈提出了一種抽象計(jì)算模型，用一個(gè)虛擬的機(jī)器代替人們進(jìn)行數(shù)學(xué)運(yùn)算，圖靈幾乎憑借自己一己之力掀起了一場(chǎng)技術(shù)革命，這場(chǎng)技術(shù)革命可以與印刷術(shù)、蒸汽機(jī)的發(fā)明和使用相提并論。

人何以為人？

到了最后，片中給我們提出一個(gè)問(wèn)題：既然有以數(shù)理邏輯為基礎(chǔ)的計(jì)算機(jī)運(yùn)行的如此之好，甚至發(fā)展出了人工智能邏輯，那人類的命運(yùn)會(huì)如何？人和機(jī)器的區(qū)別在哪里？

戴夫·克里夫，這位計(jì)算機(jī)學(xué)教授，雖然極其肯定邏輯對(duì)于人類進(jìn)步的偉大意義，但他依然堅(jiān)信人類一定是獨(dú)特的存在，是機(jī)器學(xué)不來(lái)的，比如利他主義、創(chuàng)造力以及愛。

這就是《邏輯的樂(lè)趣》這部紀(jì)錄片。

相信沒(méi)有人會(huì)拒絕一部能讓自己感到更聰明的節(jié)目，這部一次性包含數(shù)學(xué)、邏輯學(xué)、哲學(xué)等知識(shí)的紀(jì)錄片，成功做到了這一點(diǎn)。

這部紀(jì)錄片，如果結(jié)合BBC出品的其他的the joy of? …系列享用更佳，比如《數(shù)據(jù)的樂(lè)趣》（the joy of data）、《贏的樂(lè)趣》(the joy of winning)、《人工智能的樂(lè)趣》(the joy of AI)。

尤其值得稱道的是，這部紀(jì)錄片形式新穎。為了說(shuō)明邏輯學(xué)中的抽象概念，BBC用了很多搞怪賣萌的方式，比如在介紹三段論的時(shí)候，介紹弗雷格和羅素的學(xué)術(shù)交流的時(shí)候，給原本枯燥、不太好懂的紀(jì)錄片增加了很多樂(lè)趣。

但這部紀(jì)錄片意義，不僅僅向我們介紹了邏輯的意義和重要性；更重要的是，它啟發(fā)了我們：如何去培養(yǎng)孩子的邏輯思維能力。

如何培養(yǎng)孩子的邏輯能力

因?yàn)檎考o(jì)錄片名字叫《邏輯的樂(lè)趣》，但是其實(shí)它只談到了形式邏輯。所謂形式邏輯，簡(jiǎn)單粗暴的理解就是這部紀(jì)錄片中說(shuō)的計(jì)算機(jī)的工作方式。

形式邏輯是邏輯學(xué)中主流的主流，重要性不再贅言。培養(yǎng)孩子形式邏輯的最好方式，就是片中所說(shuō)的編程了。

從編程入手，培養(yǎng)孩子邏輯思維能力的想法，50年前就有了。

1968年，麻省理工學(xué)院教授、人工智能先驅(qū)西蒙派·珀特就在皮亞杰的啟發(fā)下，開發(fā)了LOGO編程語(yǔ)言，這項(xiàng)編程語(yǔ)言訓(xùn)練出了大量的科學(xué)家，也對(duì)喬布斯、保羅·艾倫、比爾·蓋茨等人產(chǎn)生了非常重要的引導(dǎo)作用。

2006年，珀特的學(xué)生米切爾·瑞斯尼克開發(fā)出了一門新的編程語(yǔ)言——Scratch。

具體如何學(xué)，我們之前寫過(guò)一篇專門文章分享：《不用報(bào)班、完全免費(fèi)，MIT專為孩子開發(fā)的編程軟件，趕緊玩起來(lái)！》，大家可以點(diǎn)擊看看。

還有一種培養(yǎng)孩子形式思維，比較有趣的方式：數(shù)獨(dú)。誕生300多年依然具有頑強(qiáng)的生命力，號(hào)稱高智商人士都喜歡玩的游戲。對(duì)了，公號(hào)對(duì)話框里回復(fù)“數(shù)獨(dú)”，可以獲取上萬(wàn)道練習(xí)題，帶著孩子玩玩看。

然而形式邏輯只是邏輯的一部分， 還有一種與我們?nèi)粘Ｉ钪嘘P(guān)系密切的邏輯——非形式邏輯，片中并沒(méi)有講到。

所謂非形式邏輯，經(jīng)常有一些其他代稱，比如“實(shí)用邏輯”、“批判性思維”、“日常邏輯”等等。

與形式邏輯不同，非形式邏輯側(cè)重點(diǎn)在于日常語(yǔ)言論證，主要運(yùn)用在政治辯論、法律訴訟、社會(huì)評(píng)論和大眾媒體的評(píng)判中。

畢竟大多數(shù)人的生活學(xué)習(xí)距離數(shù)理邏輯比較遠(yuǎn)，而距離日常邏輯比較近。而在日常邏輯中，人們并不關(guān)心論證和推理是否邏輯嚴(yán)密，只在乎前提能否對(duì)結(jié)論提供足夠的支持。從這一點(diǎn)看，非形式邏輯大為有用。

如果還是覺得非形式邏輯太過(guò)抽象的話，有另外一個(gè)詞，雖說(shuō)不太準(zhǔn)確，但能涵蓋非形式邏輯的大部分內(nèi)容，就是我們經(jīng)常說(shuō)的“批判性思維”。

那怎樣培養(yǎng)孩子的批判性思維呢？美國(guó)哲學(xué)學(xué)會(huì)曾給出一些關(guān)于分享培養(yǎng)孩子批判性思維的小貼士，這里分享給大家。

?

1. 從小啟蒙

孩子們可能暫時(shí)沒(méi)有準(zhǔn)備好學(xué)習(xí)正式的邏輯課程，但是我們可以教他們?nèi)绾螢樽约旱慕Y(jié)論提供論據(jù)，他們也可以自己學(xué)著去思考他人給出的理由和論據(jù)。

比如，從最簡(jiǎn)單的“我餓了，我想吃飯；我困了，我想睡覺開始”，從小就培養(yǎng)孩子的邏輯意識(shí)。

2. 避免教條

當(dāng)我們告訴孩子要按照某種特定方式去做時(shí)，一定要給出這樣做的理由。避免權(quán)威、武斷式的下命令：“為什么要這樣做？因?yàn)槲沂悄銒寢屟剑　?

3. 鼓勵(lì)孩子問(wèn)問(wèn)題

當(dāng)孩子對(duì)某件事不同意或表示反對(duì)時(shí)，不要著急，鼓勵(lì)孩子說(shuō)出反對(duì)意見或者他認(rèn)為的難處。

審視猶太人的教育理念，會(huì)發(fā)現(xiàn)其中的精髓——“提問(wèn)—討論”式的學(xué)習(xí)方式。他們認(rèn)為，“你問(wèn)我答、我問(wèn)你答”的討論，可以讓自己的想法推陳出新，這才是真正的學(xué)習(xí)（想深入了解猶太人的學(xué)習(xí)方式可以看看之前的這篇文章—>什么才是最好的學(xué)習(xí)方式？四個(gè)哈佛學(xué)生的“終極追問(wèn)”，答案一點(diǎn)也不意外）。

4. 鼓勵(lì)孩子再多思考一點(diǎn)

孩子能想到正確答案當(dāng)然好了，但并不是所有的問(wèn)題都只有一個(gè)答案，多多鼓勵(lì)孩子思考其他的解釋和解決方案，這樣他們思考問(wèn)題會(huì)更加靈活。

5.鼓勵(lì)孩子表述新概念

當(dāng)有一個(gè)新的概念出現(xiàn)時(shí)，鼓勵(lì)孩子用他們自己的話來(lái)說(shuō)出來(lái)，并且鼓勵(lì)孩子做有意義的區(qū)分。

6. 和孩子討論偏見問(wèn)題

即便是比較小的孩子也能理解情緒、動(dòng)機(jī)甚至渴望都可能影響人類的判斷，所以勇敢大膽的評(píng)價(jià)吧。

比如，和孩子討論胖和瘦，美和丑，富和窮的問(wèn)題。

7. 鼓勵(lì)孩子寫作

寫作可以幫助學(xué)生加深思考并且提升他們批判性思考的深度。在一項(xiàng)研究中，研究人員將學(xué)生分為兩組。

一組必須對(duì)他們?cè)趯?shí)驗(yàn)室的成果進(jìn)行書面說(shuō)明，對(duì)照組則是進(jìn)行簡(jiǎn)短的回答和測(cè)驗(yàn)。學(xué)期結(jié)束后，寫作組的學(xué)生，很明顯分析能力有了很大提高，而對(duì)照組的沒(méi)有。

因此鼓勵(lì)孩子寫作，把自己的觀點(diǎn)和理由寫下來(lái)，是一項(xiàng)很好的練習(xí)批判性思維能力的方式。

都說(shuō)“授人以魚不如授人以漁”，對(duì)于孩子的成長(zhǎng)和未來(lái)發(fā)展來(lái)說(shuō)，這“漁”就是邏輯思維能力。

當(dāng)然，它不會(huì)是孩子生活的全部，但肯定是其中最重要、最基礎(chǔ)的一環(huán)。尤其，在計(jì)算機(jī)、AI等等高新技術(shù)均以邏輯為根本的現(xiàn)在，孩子邏輯思維能力的培養(yǎng)，已經(jīng)不再是高層次要求，而是基本要求。

所以，一直覺得，相比超前學(xué)習(xí)課程，多培養(yǎng)幾個(gè)特長(zhǎng)才藝，基本能力，包括邏輯思維能力的培養(yǎng)更為重要和關(guān)鍵。缺少這一環(huán)，才真的會(huì)讓孩子“落后”在起跑線上。

聲明：本文章由網(wǎng)友投稿作為教育分享用途，如有侵權(quán)原作者可通過(guò)郵件及時(shí)和我們聯(lián)系刪除